यत्र–तत्र–सर्वत्र 'नम्बरै नम्बर'
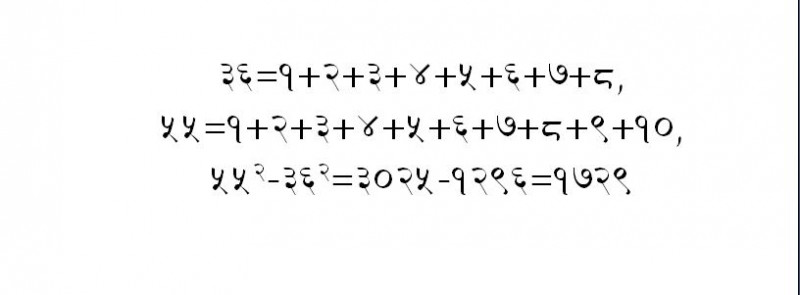
नम्बर सञ्चार जगत्को शक्तिशाली तथा प्रेरक औजार हो। वाणिज्य, व्यवसायको फाँटमा पनि नम्बर अमूल्य औजार साबित भएको छ। नम्बरले जस्तो मीठो ढङ्गले अरु केही कुराले काम गर्दैन। यसका दोष वा सीमा पनि छन्। नम्बरसँगै हिड्दा धेरै खाल्डाखुल्डी पनि भेटिन्छन्। नम्बरलाई विनाविवेक प्रयोग गर्दा यसबाट हानि हुनसक्छ। प्रयोग गर्न जान्नुपर्छ, नम्बरले हाम्रो जीवनमा सुधार ल्याउन मद्दत गर्छ।
नेपालीमा गन्ती बुझाउने सङ्ख्या शब्दको अर्थमा अङ्ग्रेजीको ‘नम्बर’ (Number) प्रयोग हुने गरेको छ। अङ्ग्रेजीबाट रुप नफेरिई जस्ताको तस्तै आएको यो शब्दलाई नेपाली जनबोलीले स्वीकार गरिसकेको छ। प्रयोगका हिसाबले पनि यो शब्द सङ्ख्या जत्तिकै चल्तीमा छ। ‘उसले एक नम्बरमा नाम निकाल्यो’ भनेको सुन्दा हामीलाई सजिलो लाग्छ। ‘उसले एक सङ्ख्यामा नाम निकाल्यो’ भन्दा केके नमिले जस्तो लाग्छ। सञ्चार माध्यमले पनि नम्बर शब्दलाई उत्तिकै मन पराउँछन्- ‘अवैतनिक दूतलाई फेरी झन्डा र नीलो नम्बर प्लेट’।
नेपालका कानून, पुस्तक, पत्र–पत्रिका आदिमा नम्बर शब्दको प्रयोग व्यापक छ। नम्बरको विशेषण ‘नम्बरी’ शब्द पनि वर्षौं देखि चल्तीमा छ-पहिलेपहिले सरकारले विशिष्ट पण्डितलाई नम्बरी पण्डितको मान दिने चलन रहेछ। सय रुपैयाँको नोटलाई नम्बरी नोट पनि भनिन्छ। असल दर्जाको सुन नम्बरी हुन्छ। तर जीविकोपार्जनका निम्ति गरिएको भए तापनि ‘दुई नम्बरी’ धन्दालाई राम्रो पेशा मानिँदैन। ‘नेपाली जिभ्रामा पचिसकेको’ मानेर नम्बर र नम्बरी दुवै शब्दलाई नेपाली शब्दकोशले प्रविष्टि दिएको छ।
कथ्य र लेख्य दुवैमा नम्बर र सङ्ख्या शब्द सराबरी प्रयोग हुने गरेका छन्। लोकसेवा आयोगले निकाल्ने सूचना यसको उदाहरण हो। आयोगको एउटै सूचनामा यी दुई शब्दको छ्यासमिस प्रयोग भेटिन्छ- ‘सूचना नम्बर, विज्ञापन नम्बर, वर्णानुक्रम नम्बर, रोल नम्बर, माग पद संख्या, लिखित परीक्षामा सम्मिलित संख्या, अन्तर्वार्ताका लागि छनोट भएको संख्या‘। शिक्षा मन्त्रालयको सूचनामा पनि त्यस्तै छ्यासमिस भेटिन्छ- ‘गणितको परीक्षामा १०० पूर्णाङ्कमा ९५ भन्दा बढी नम्बर ल्याउने विद्यार्थी संख्या’।
अङ्ग्रेजी नम्बर शब्दको यतिको ‘बखान’ गर्नुपर्नाको विशेष कारण छ। यसको उद्देश्य‘सङ्ख्यालाई नम्बरले लतारेको छैन’ भन्ने सङ्केतका लागि हो। अर्थात्, नम्बरसँग यसरी काँध–मा–काँध मिलाएर चल्तीमा रहेको सङ्ख्या शब्द ‘अङ्ग्रेजीबाट लतारिएको’ छैन ।
यो पुस्तकमा पनि नम्बर र सङ्ख्या शब्द एक अर्काको सट्टामा सराबरी प्रयोग भएका छन्। प्रसिद्धिका आधारमा नम्बरलाई ‘गणितीय, सांस्कृतिक, ऐतिहासिक’ आदि विभिन्न वर्गमा छुट्ट्याउने चलन छ। यो परिच्छेदमा नम्बरको गणितीय पक्षमा जोड दिइएकोछ।

नम्बर अनुपम छ। ग्रीक दार्शनिक पाइथागोरसका अनुयायीहरुले त ‘ब्रम्हाण्ड नै नम्बरले व्याप्त छ’ भन्ने निष्कर्ष निकालेका थिए। मानव सभ्यता विकासको सुरुआतदेखि नै नम्बरले मानिसलाई मोहित बनाउँदै आएको छ। नम्बर र मानिसको सम्बन्ध अचम्मको छ। उसले नम्बरलाई मायाँसँगसँगै हेलाँ गर्दै आएको छ। एकातिर नम्बरबाट उसले धेरै अपेक्षा गर्छ भने अर्कोतिर यसलाई उपेक्षा गर्न पनि छोड्दैन।
हामी नम्बरै नम्बरले घेरिएका छौं- यत्र–तत्र–सर्वत्र नम्बरै नम्बर! जन्मेको दिनदेखि नम्बर हामीसँगै हिँड्न थाल्छ। सधैँ हाम्रो जिन्दगी वरपर घुमिरहन्छ। हामीलाई मन परोस् या नपरोस् यसले हामीलाई रतीभर छोड्दैन। रात वा अँध्यारोमा बरु छायाँले छोड्ला तर यसले हामीलाई एक्लै छोड्दैन। सचेतन वा अर्धसचेतन जुनसुकै अवस्थामा पनि नम्बर हाम्रो साथमा रहन्छ।
जीवन चर्यामा कहीँ न कहीँ हामी नम्बर प्रयोग गरिरहेका हुन्छौं। जानाजान वा अनजानमा समय, मिति, साल, मौसम आदि बताउन नम्बर प्रयोग भैरहन्छ। घरपरिवारको कुरा गर्यो नम्बर, पसल गयो नम्बर, समाचार सुन्यो नम्बर, जता फक्र्यो उतै नम्बर! जस्तै-हाम्रो परिवारमा ७ जना छौं; एक धार्नी आलु चाहियो; करीब ४ किलोमीटर टाढा छ; ऊ आइपुगेको करीब दुई घण्टाभयो; दुई हजार दुई सय ३७ जनामा कोरोना देखियो आदि।
केही नम्बरहरूलाई हामीले सधैं सम्झनु आवश्यक हुन्छ। टेलिफोन, नागरिकता र पासपोर्टका नम्बरहरू हाम्रो सहज पहुँचमा राख्नुपर्छ। अस्पताल, एम्बुलेन्स, रेडक्रस, ब्लडबैंक, दमकल, पुलिस आदिको सुविधा पाइने ठाउँमा आपत्कालीन नम्बरहरूको महत्व बढ्दो छ। क्रेडिटकार्ड, डेबिटकार्ड, एटीएम कार्ड नम्बरहरू त सधैं गोप्य र सुरक्षित राख्नुपर्छ। केही भविष्यवादीहरू त ‘अब नम्बरसँग बाँच्ने होइन नम्बरले बाँच्ने दिन आए’ भन्न पनि हिचकिचाउँदैनन्। उनीहरूले भनेका छन्-‘भविष्यमा नामको मतलव हुनेछैन, सिक्युरटि नम्बर वा राष्ट्रिय परिचय पत्र नम्बरले नै काम तमाम गर्ने छ’।
समय अनन्त छ। समय आफ्नै गतिमा चल्छ, कसैलाई पर्खदैन र टेर्दैन पनि। हामी नै समयको पछिपछि दगुर्नु पर्छ। ‘कालश्य वशगाः सर्वे न कालः कस्यचिद्वशः’ अर्थात् सबै समयको अधीनमा छन्, समय कसैको अधीनमा छैन। यस्तो बलवान् समयको नापलिन नम्बर नै अघि सर्छ- ‘म ३६ वर्षको भएँ’; ‘चिनीयाँ भाषामा महाभारतको अनुवाद ईसाभन्दा दुई सय वर्ष पहिले नै भएको थियो’; ‘आउँदो छ महिनाका लागि पुग्ने इन्धन मौज्दात छ’ आदि।
यस्तो साह्रै उपयोगी र बलवान् नम्बर आफैं भने बोल्दैन। अमेरिकी स्ट्याटिस्टिशन अर्थात् साङ्ख्यिकीविद् सिल्भर (Nate Silver)ले भनेका छन्- ‘नम्बरसँग आफ्नोबारे बोल्नलाई सहज उपाय छैन। हामीले नम्बरको लागि बोलिदिनुपर्छ; हामीले नै अर्थ भरिदिनुपर्छ।’ प्रसङ्गविनाको नम्बरले काम लाग्ने सूचना दिदैन। यसकारण, साङ्ख्यिकीमा उपयोगी बनाउन नम्बरलाई ठीक र स्पष्ट तरीकाले अथ्र्याउनु जरुरी हुन्छ।
शब्दले स्पष्ट नपारेसम्म नम्बर अनगिन्ती आशयमा अलमलिई रहन्छ। लेबल, समय, एकाइ आदि नखुलेसम्म नम्बर लगभग निरर्थक, दिशाविहीन अनि बेकारको हुन्छ। कुनै काममा आउँदैन- ‘बाँदरको पुच्छर, लौरो न हतियार!’ कसैले १ मात्र भन्यो भने के बुझ्ने?- एकजना, एकवर्ष, एककिलोमीटर,एकघण्टा, एकप्रतिशत आदि जे पनि हुन सक्छ। त्यस्तै, ‘१.९५’ ले के बुझाउँछ? थप शब्दले नकिटेसम्म कुन विषयको सूचक हो भन्ने निश्चित हुँदैन- जनसङ्ख्या वृद्धिदर, प्रजननदर, कुल गार्हस्थ्य उत्पादन(जीडीपी) वृद्धिदर, मूल्य वृद्धिदर, कुनै भाषा बोल्ने जनताको प्रतिशत आदि जे पनि हुन सक्छ।
जाडोल (Jadoul)ले एकाइविनाको नम्बरलाई ‘नाङ्गो वा ठिङ्गो’भनेका छन्। नाङ्गो नम्बरको अर्थ हुँदैन। लेबल, एकाइ, स्रोत आदिको लुगा लगाएर प्रस्तुत गर्यो भने मात्र नम्बर सार्थक हुन्छ। ग्रीक दार्शनिक प्लेटोले २४ सय वर्ष अगाडि नै भनेका थिए- ‘निर्णय गर्दा ठिङ्गो नम्बरको आधारमा होइन सूचनाको आधारमा गर्नुपर्छ।’
उपर्युक्त १.९५ नम्बरलाई यो जीडीपीको वार्षिक वृद्धिदर हो भनेर किटेपछि अर्थ खुल्नथाल्छ। प्रतिशत शब्दले यसलाई थप स्पष्टपार्छ। पहिले कुनै प्रसङ्गमा नआएको भए हुलियाका लागि यी विवरण पनि खुलाउनु पर्छ- समय,क्षेत्र, मूल्यको प्रकार, अनुमानको प्रकार, अनुमान विधि आदि।
यसो भन्न सकिन्छ- अन्तिम अनुमानअनुसार आर्थिक वर्ष २०५७/५८ को स्थिर मूल्यको आधारमा आ. व. २०७१/७२ मा नेपालको जीडीपीको वार्षिक वृद्धिदर १.९५प्रतिशत थियो। यसरी विवरण थपेपछि बल्ल यो उपयोगी सङ्ख्येय-सूचना बन्छ। दैनिक व्यवहारमा भने यसरी विस्तृत विवरण दिने चलन छैन। छापामा यस्ता शीर्षक भएका समाचार आउँछन्- ‘विश्व बैंकले सन् २०२० मा आर्थिक वृद्धिदर ६.५मा सीमित रहने प्रक्षेपण गरेको छ।’
समय अनुसार नम्बरको मान फरक पर्छ। नेपालमा २०सौं शताब्दिको शुरुतिर हजारियालाई सेठ मानिन्थ्यो। एक्काइसौं शताब्दिको शुरुमा आइपुग्दा दश लाखलाई पनि ठूलो सङ्ख्या मान्न छोडियो। आजकल लखपतिहरु नै लाखौं भैसके। अहिले करोडपति, अर्बपतिहरु धनाढ्यमा गनिन्छन्। एकाइको फरकले पनि सङ्ख्याको मानमा आनका तान फरक पर्छ ।७० किलोमीटर प्रतिघण्टा र ७० माइल प्रतिघण्टाको गतिमा धेरै फरक पर्छ।
अर्थको आधारमा नम्बरदुई किसिमका छन्- ठ्याक्कै र करीब। पहिलो किसिमको नम्बर पूर्णतया निश्चित हुन्छ। यसलाई हेरफेर गर्ने वा छोट्याउने कुरा हुँदैन। एक हप्तामा ठ्याक्कै ७ दिन हुन्छन्, न घटी न बढी। परिभाषाअनुसार, एक रोपनीमा ठ्याक्कै पाँच हजार चार सय ७६ वर्गफीट हुन्छ। एक बिघामा ठ्याक्कै ७२ हजार नौ सय वर्गफीट हुन्छ।
करीब भनेको लगभग अर्थात् झण्डैझण्डै त्यति हो। यस्तो नम्बरमा कुनै निश्चितता हुँदैन। सुन, चाँदीका गहनाको तौल अक्सर तोलामा हिसाब गर्ने चलन छ। एक तोलालाई ग्रामको एकाइमा परिवर्तन गर्दा ११.६६३८०८ ग्राम हुन्छ। व्यवहारमा सजिलो बनाउन यसलाई छोट्याएर करीब ११.६६ ग्राम वा ११.७ ग्राम मान्ने गरिन्छ।
जग्गा नापमा एकबिघा बराबर १३.३१२६३६९६१२... रोपनी हुन्छ। आमप्रयोगकर्तालाई यो लम्बेतान सङ्ख्या बुझ्न सजिलो छैन। व्यवहारमा ल्याउन यसलाई गणितीय उपायले छोट्याउनुपर्छ। दशमलव पछाडि पाँचोटा अङ्क लिएर छोट्याउदा १३.३१२६४, अनि दुइटा अङ्कसम्म मात्र लिँदा १३.३१ हुन्छ। यसरी आवश्यकताअनुसार ‘गोल’ सङ्ख्यामा बदलेर छोट्याउने विधिलाई अङ्ग्रेजीमा ‘Rounding’ भनिन्छ। यसरी छोट्याएर बनाएको गोल सङ्ख्याको अगाडि करीब लेख्नु पर्छ- अर्थात्, एक बिघामा करीब १३.३१ रोपनी हुन्छ।
करीब १३.३१ रोपनी भनेको १३ रोपनी, पाँच आना र करीब एक पैसा हो। विशेष अवस्थामा बाहेक यसलाई १३ रोपनी पाँच आना चानचुन भने पुग्छ। अझ सजिलो पार्न यसलाई करीब सवा तेह्र रोपनी भन्न सकिन्छ।
धेरैले अङ्क र सङ्ख्यालाईपर्याय मान्छन् अर्थात् उस्तै अर्थमा लिन्छन्। तर पारिभाषिक अर्थमा यी दुई शब्दको आशय फरक छ। अङ्कले एक, दुई, तीन आदि जनाउने चिह्न (Symbol)लाई बुझाउँछ। एकदेखि नौसम्मको कुनै सङ्ख्या जनाउन पनि अङ्कको प्रयोग गरिन्छ। सङ्ख्या भनेको कुनै वस्तु गन्ती गर्दा लेखिने वा भनिने एउटै अङ्क वा अङ्कहरुको समूह शब्द हो। गणनाक्रममा कुनै वस्तुको मात्रा बुझाउन सङ्ख्या शब्दको प्रयोग हुन्छ। गणनाबाट निस्कने परिणामलाई पनि सङ्ख्यामा व्यक्त गरिन्छ । उदाहरण- अङ्क भनेको ०, १, २, ३, ४, ५, ६, ७, ८, वा ९ मध्ये कुनै एक चिह्न हो। एक वा अनेक वर्णहरु मिलेर शब्द बनेजस्तै एक वा सो भन्दा बढी अङ्कहरु मिलेर सङ्ख्या बन्छ। १९५१ र ०.१९५१ दुवै चार अङ्कले बनेका सङ्ख्या हुन्। सात दिनमा ‘७’ एकअङ्के सङ्ख्या हो।
नागरिकता नम्बर, लालपूर्जा नम्बर, मोबाइलफोन नम्बर आदि ‘गणितीय सङ्ख्या हुन् कि होइनन्?’ भन्ने प्रश्नको उत्तरमा पण्डितहरु एकमत छैनन्। गणितज्ञहरुका अनुसार, सङ्ख्या भने पछि जोड, घटाउ, गुणन वा भाग गर्न सकिने हुनुपर्छ। फोन नम्बरलाई यसो गर्नुको कुनै अर्थ हुँदैन। तर धेरै अङ्क मिलेर बनेको हुँदा यसलाई सङ्ख्या नै मान्नु पर्छ भन्नेहरु धेरै छन्।
सङ्ख्याको प्रारम्भ १, २ आदिबाट हुन्छ, शून्यबाट होइन। एक्लो शून्य सङ्ख्या होइन, अङ्क हो। एक, दुई आदि अङ्कसँग मिसिएर यो सङ्ख्याको अङ्ग बन्छ। राष्ट्रकवि माधव घिमिरेले शून्यलाई ‘नौ अङ्क पछिको प्राप्ति’ भनेका छन्। प्राचीन धर्मग्रन्थहरुले पनि शून्यलाई अङ्कको समूहमा राखेको भेटिन्छ। गोबर्धनपीठ पुरीका शङ्कराचार्य स्वामी श्रीनिश्चलानन्द सरस्वतीले भनेका छन्- ‘शुक्रनीतिले शून्यलाई अङ्क मानेको छ’।
‘आँकडा’ (डेटा) साङ्ख्यिकीसँग जोडिएर आउने पारिभाषिक शब्द हो। कुनै व्यक्ति, वस्तु, विषय, स्थान, घटना, अवस्था, कार्य आदिका सम्बन्धमा सङ्कलित विवरणलाई आँकडा भनिन्छ। वर्णनका दृष्टिले आँकडा दुई प्रकारका छन्- मात्रात्मक र गुणात्मक। व्यक्तिको उमेर मात्रात्मक हो भने लिङ्ग छुट्याउने आँकडा गुणात्मक हो। गुणात्मक विवरण शाब्दिक हुन्छ। लगत प्रशोधन गर्नुपर्दा यस्तो आँकडालाई उपयुक्त अङ्कसङ्केत वा कोडमा बदलिन्छ। जस्तै-पुरुषलाई १ र महिलालाई २ को कोडमा बदलेर लगत प्रशोधनलाई सहज बनाइन्छ। यसकारण आँकडा सङ्ख्या हुन जरुरी छैन।
विस्तारित तहकादृष्टिले डेटा तीन किसिमका छन्- माइक्रोडेटा, म्याक्रोडेटा, र मेटाडेटा। व्यक्तिगत वा एकाइ तहको विवरण माइक्रोडेटा हुन्छ। कुनै गणना वा सर्वेक्षणमा व्यक्तिपिच्छे सङ्कलन गरिएको विवरण सहितको लगत माइक्रोडेटा हो। माइक्रोडेटाबाट गन्ती जोडेर वा औसत निकालेर म्याक्रोडेटा बनाइन्छ। मेटाडेटाले डेटाबारे विवरण खुलाएर सूचना दिन्छ। मेटाडेटामा गणना वा सर्वेक्षण विधि, माइक्रोडेटाको गुणस्तर आदिको विवरण हुन्छ।
सामान्यतः आँकडा र साङ्ख्यिकीलाई उस्तै अर्थ दिने शब्दका रुपमा हेरेको भेटिन्छ। दैनिक बोलीचालीमा त साङ्ख्यिकी, आँकडा वा विवरणर सूचना शब्दको सराबरी प्रयोग हुने गरेको छ। तर पारिभाषिक दृष्टिले आँकडाको भन्दा साङ्ख्यिकीको तह माथि हुन्छ। साङ्ख्यिकी भन्दा सूचना अरु एक तह माथि हुन्छ। फरक देखाउन आँकडालाई ‘कोरामाल’ भन्ने पनि चलन छ। आँकडालाई सूचना उत्पादन प्रणालीमा सबैभन्दा सानो एकाइ मानिन्छ। आँकडालाई साङ्ख्यिकीको केन्द्रीय स्वरुप एवं विशेषता मानिन्छ। अर्थात् अक्सर कोरामालको रुपमा आँकडाएकत्रित गरेर साङ्ख्यिकी उत्पादन गरिन्छ । परिमार्जन सहित मूल्य थप र विश्लेषण गरेपछि उपभोग्य सूचना उत्पादन हुन्छ । सूचनालाई परिबन्द र प्रसङ्ग मिलाएर उपयोग गरिन्छ।
नौलो कुरा होइन, एकअङ्के सङ्ख्याको मान नौ वा सोभन्दा कम हुन्छ। दुई वा सोभन्दा बढी अङ्क मिलेर बनेका सङ्ख्यामा अङ्कले ओगटेको स्थानअनुसार मान फरक पर्छ। अर्थात्, उही अङ्क अगाडि, पछाडि वा बीचमा आउँदा सङ्ख्याको मान फरक पर्छ- १७५, ५१७, ७५१ आदि। सङ्ख्याको बनोटमा अङ्क थपिदै जाँदा मान पनि बढ्दैजान्छ। पाँच अङ्कले बनेको सङ्ख्या हजारमा सीमित हुन्छ भने दशअङ्के सङ्ख्या अर्बसम्म पुग्छ।
शून्य र एकअङ्के सङ्ख्याका धार्मिक एवं सांस्कृतिक महत्व पनि छन्। विभिन्न धर्ममा यी सङ्ख्याको आआफ्नै किसिमले महत्व देखाइएको भेटिन्छ। हिन्दू धर्ममा शून्यलाई निर्गुण, निराकार ब्रह्मको प्रतीक मानिन्छ। बौद्ध धर्ममा शून्यताको विशेष महत्व छ। सङ्ख्या एकले अद्वैतवादलाई सङ्केत गर्छ भने दुईले द्वैतवादको सिद्धान्त जनाउँछ। ब्रह्मा, विष्णु, महेश्वरको संयुक्त रुपलाई त्रिमूर्ति भनिन्छ। चारले सृष्टिको चौथो पक्ष बुझाउँछ। पञ्चमहाभूतसँग पाँच सम्बन्धित छ। छ मुख भएका कुमारलाई षडानन भनिन्छ। सप्ताह–पुराण सात दिनमा सम्पन्न गरिन्छ। अष्टचिरञ्जीवीमा दीर्घजीवी मानिएका आठ ऋषिमुनिको नाम आउँछ। नौ सबै भन्दा ठूलो एकअङ्के सङ्ख्या हो; नवग्रहलाई शुभाशुभ फलका दाता मानिन्छ। एकअङ्के सङ्ख्याको उदाहरण तालिका १.१ मा दिइएको छ।
एकअङ्के सङ्ख्याका आआफ्नै विशेषता छन्। जस्तै- सङ्ख्या ‘६’ को अप्रतिम विशेषता छ। १, २ र ३ जोड्दा वा गुणनगर्दा ‘६’ नै आउँछ (१+२+३=६;१×२×३=६)। जुनसुकै सङ्ख्यालाई ९ ले गुणागर्दा आएको गुणनफललाई एक अङ्कसम्म लैजाँदा जहिलेपनि ९ नै बाँकी रहन्छ- '(७×९=६३, ६+३=९); (११×९=९९, ९+९=१८,१+८=९), (४५×५६=२५२०, २+५+२+०=९)।'
दुई वा सो भन्दा बढी अङ्क मिलाएर एक भन्दा बढी सङ्ख्या बनाउन सकिन्छ। उदाहरणार्थ, २, ०, १ र ९ यी चार अङ्कले बनेको सबैभन्दा ठूलो र सबैभन्दा सानो सङ्ख्या हेरौं- ९२१० सबैभन्दा ठूलो सङ्ख्या हो भने १०२९ सबैभन्दा सानो सङ्ख्या हो। परिभाषाअनुसार ०१२९ तीन अङ्कले बनेको सङ्ख्या हो।
आजकल शून्य वा सुन्नालाई सहज रुपमा लिने गरिन्छ। तर इतिहासका अनुसार गणितमा शून्य नवीन आविस्कार हो। पुरातन समाजलाई शून्यको आवश्यकता थिएन। बेबिलोनियन तथा रोमनहरुसँग शून्यलाई जनाउने कुनै चिन्ह थिएन। ग्रीकहरुको पनि थिएन। उनीहरु शून्य वा खालीखण्डलाई अङ्क मान्दैनथे। जटिल समस्या समाधानगर्न विभिन्न किसिमका चिह्न प्रयोग गरिन्थे। यसकारण उनीहरुलाई शून्यको चासो भएन, यसको खोजीनिती भएन।
त्यसबेला शून्यको सट्टा रित्तो वा खालीको अवधारणाले कामगर्दै आएको थियो। किसानको खोरमा दुइटा बाख्रा रहेछन्। राती दुवैलाई बाघले लगेछ, खोर खाली भयो। खाली अवस्था जनाउन कुनै चिह्न आवश्यक ठानिएन। यसकारण त्यस बेलाका गणितज्ञले अङ्क परिवारमा शून्य समावेश गर्नेतर्फ ध्यान नदिएका होलान्। तर शून्यको आविस्कार नहुँदासम्म गणितको विकास सीमित रह्यो।
भनिन्छ, सबैभन्दा पहिले पूर्वमा शून्यको ‘अवधारणा’ विकास भएको हो। त्यसपछि यो पश्चिमतर्फ बढ्दै गयो। पहिलो पटक भारतीय गणितज्ञले शून्यको आवश्यकता महसूस गरे र यसको अभिलेख तयार पारे। खाली वा रित्तोपना बुझाउन बाहेक अरु उपयोगका लागि पनि शून्यको आवश्यकता महसूस हुँदै गयो। अङ्क–लहरको विभिन्न स्थानमा शून्य घुसाउँदा सङ्ख्याको मान परिवर्तन हुन्छ भन्ने कुरा थाहा भयो। त्यसपछि सङ्ख्याको मान परिवर्तनका लागि शून्यको प्रयोग हुन थाल्यो। ३०७, ३७०, ३००७ र ३७०० को मान फरक छ। तर शून्यको अभावमा यी सबै ३७ मा झर्छन्। यसकारण, शून्यलाई ‘स्थानग्राही’ भनिन्छ।
शून्य केवल स्थानग्राही भने होइन । यसले गणितमा ‘धनात्मक’र ‘ऋणात्मक’ सङ्ख्या बीच सिमाना पनि निर्धारण गर्छ- (..., –३, –२, –१, ०, १, २, ३, ...) । धनात्मक सङ्ख्याको लहरमा बायाँ लाग्दा शून्य भेटिन्छ, त्यसपछि ऋणात्मक सङ्ख्याको लहर शुरु हुन्छ। ऋणात्मक लहरमा दाहिनेतर्फ आउँदा फेरी शून्य भेटिन्छ।
आर्य भट्ट प्राचीन भारतका प्रख्यात गणितज्ञ हुन्। उनले पाँचौं शताब्दिमा ‘आर्यभाटीया’ नामको ग्रन्थ लेखे। आर्य भाटियाको ‘गणितपाद’ खण्डमा उनले स्थानमान निर्धारणमा शून्यको महत्व उल्लेख गरेका छन्-
एकं च दशं च शतं च सहस्रं त्वयत नियुते तथा प्रयुतं ।
कोट्यर्वुदं च वृन्दं स्थानात् स्थानं दशगुणं स्यात् ।।
अर्थात् एक, दश, सय, हजार, अयुत (दश हजार),नियुत (लाख), प्रयुत (दश लाख), कोटी (करोड), अर्वुद (दश करोड), र वृन्दा (अर्ब)- प्रत्येक अघिल्लो सङ्ख्या भन्दा दश गुणा बढी हुन्छ। यसरी शून्यले दशको सङ्ख्या निर्माण गर्यो।
सातौं शताब्दिमा भारतवर्षका अर्का प्रसिद्ध गणितज्ञ ब्रम्ह गुप्तले शून्यको अङ्क गणितीय नियमहरु निर्धारण गरे। जुनसुकै सङ्ख्यामा शून्य जोड्दा वा घटाउँदा सङ्ख्याको मान परिवर्तन हुँदैन (३७+०=३७ अनि ३७–०=३७)। जोड र घटाउ क्रियामा यसरी शान्त रहने शून्य गुणन क्रियामा भने आक्रामक हुन्छ। गुणा गर्दा शून्यले जुनसुकै सङ्ख्यालाई पनि शून्यमा नै झारिदिन्छ (३७´०=०; ३००७´०=०)। भागहारमा भने ब्रम्हगुप्त अलमलिएका छन्। शून्यले भाग गर्दा आउने भागफललाई उनले विना परिभाषा नै छोडि दिएका छन्।
पछि १२–रौं शताब्दिमा आएर अर्का गणितज्ञ भाष्कराचार्यले आफ्नो ‘लीलावती’ नामक ग्रन्थमा शून्यको व्याख्या गरेका छन्-
योगे खं क्षेपसमं, वर्गादौ खं, खभाजितो राशिः ।
खहरः स्यात्, खगुणः खं, खगुणश्चिन्त्यश्च शेषविधौै ।।
शून्ये गुणके जाते खं, हारश्चेत् पुनस्तदा राशिः ।
अविकृत एव ज्ञेयस्तथैव खेनोनितश्च युतः ।।
भावार्थ- ‘शून्यमा कुनै सङ्ख्या जोड्दा योगफल त्यही सङ्ख्या बराबर हुन्छ। शून्यको वर्गादि (वर्ग, वर्गमूल, घन, घनमूल आदि) शून्य नै हुन्छ। कुनै राशिलाई शून्यले भाग दिँदा त्यो राशिको संज्ञा ‘खहर’ हुन्छ (कुनै राशिलाई शून्यले भाग गर्दा आउने राशिलाई खहरभनिन्छ)। कुनै राशिलाई शून्यले गुणा गर्दा गुणनफल शून्य हुन्छ। कुनै राशिलाई शून्यले गुणन गरेर शून्यले नै भाग गर्यो भने सो राशि अविकृत (जस्ताको तेस्तै) रहन्छ। शून्यको जोड, घटाउ पनि यसै प्रकारको हुन्छ ।’ भाग गर्ने प्रकृयाका सन्दर्भमा उनले दिएको परिभाषा स्पष्ट छैन।
अध्यात्मवादीहरु शून्यलाई गोलाकार वस्तुको रुपमा अथ्र्याउँछन्- ‘गर्भाशय गोलाकार हुन्छ। गर्भाशय सृष्टिको स्रोत हो। शून्य पनि सृष्टिको स्रोत हो।’ वेदले शून्यलाई ज्ञानको अन्तिम स्रोत मानेको छ। वेदले उद्घोष गरेको छ- ‘शून्य नै मानव ज्ञानको अन्तिम सीमा हो, यसपछि जान्नुपर्ने कुरा बाँकी रहँदैन। शून्य सबै कुराको अन्तिम विलयक हो।’ बौद्धमतमा ‘शून्यता’-को विशेष महत्व छ। जीवनको अन्त्यतिर महाकवि लक्ष्मीप्रसाद देवकोटालाई पनि शून्यताको अनुभूति भयो होला र त भनेका छन्- ‘म शून्यमा शून्य सरी बिलाएँ।’
विज्ञान विषयका संवाददाता रेस्निक (Brian Resnick) शून्यलाई‘दिमाग खल्बल्याउन सक्ने विचित्रको’ अङ्क ठान्छन्। उनले भनेका छन्- ‘शून्यविना आधुनिक विश्वमा धेरै कुरा रहँदैनन्। शून्यविना आधुनिक इलेक्ट्रोनिक्स अस्तित्वमा आउने थिएन। क्याल्कुलस जस्तो उत्तम गणितको विकास हुने थिएन। इन्जिनियरिङ वा अटमेशन पनि हुने थिएन। हामीले प्रयोग गर्ने कम्प्यूटर ० र १ मा आधारित प्रणालीमा विकास भएको हो।’
साङ्ख्यिकीसँग शून्यको विशेष सम्बन्ध छ। साङ्ख्यिकीका सूत्रहरु सम्भाव्यताको सिद्धान्त (Probabilty Theory)मा आधारित हुन्छन्। साङ्ख्यिकीमा कुनै घटना घट्नसक्ने संयोग अनुमान गर्न यो सिद्धान्तको मद्दत लिइन्छ। याे सिद्धान्त अनुसार ० ले ‘असम्भावना’ बुझाउँछ भने १ ले ‘निश्चितता’। बाख्रा मात्रै भएको गोठ वा बगालमा भेडो छानिने सम्भावना ० हुन्छ। अर्थात् भेडो छानिने घटना असम्भव हुन्छ।
गणितमा ‘१’ सबैभन्दा सानो पूर्ण धनात्मक सङ्ख्या हो। यो अभिवाज्य छ, यसलाई अरु सिङ्गो सङ्ख्यामा टुक्य्राउन सकिदैन। अरु कुनै धनात्मक सङ्ख्या जोडेर १ बन्दैन। अनेक अर्थमा १ अप्रतिम छ। गणितका पण्डितहरुले १ लाई ‘विशिष्ट सङ्ख्या’ मानेका छन्।
सङ्ख्या १–लाई एकताको प्रतीक मानिन्छ । ग्रीक दार्शनिक पाइथागोरसका अनुयायीहरु सङ्ख्यालाई बहुवचन मान्थे । एकवचनमा भएकोले एकलाई उनीहरु सङ्ख्या मान्दैनथे तर सबै सङ्ख्याको स्रोत यही हो भन्थे । किनभने, १ मा १ जोड्दै जाँदा जुनसुकै धनात्मक सङ्ख्या बन्छ (१+१+१=३;७७+१=७८;७८+१=७९ आदि)।
‘१’ ले सङ्ख्यालाई जोर–बिजोरमा बदल्न सक्छ। जोर सङ्ख्यामा १ जोड्दा बिजोर हुन्छ; बिजोरमा १ जोड्दा जोर सङ्ख्या बन्छ (३२+१=३३; ६४+१=६५आदि)। जोड-घटाउमा यसले जोर-बिजोर बदल्नसक्ने भए तापनि गुणा-भाग क्रियामा यो शान्त रहन्छ। जुनसुकै सङ्ख्यालाई १ ले गुणा वा भाग गर्दा सो सङ्ख्या बदलिँदैन(३७१ = ३७;२०७८१ = २०७८ आदि)। यस्तो गुण भएको सङ्ख्या यो मात्रै हो। गुणा गर्दा नबदलिने भएकोले १ को वर्ग, घन लगायत सबै उच्च तहको मान पनि बदलिँदैन (!@ = १*१ = १; !# = १*१*१ = १ आदि)। अङ्क‘०’-को पनि यस्तै गुण छ।
आध्यात्मिक चिन्तनमा १ लाई ईश्वर वा ब्रह्माण्डको प्रतीक भनिएको छ। ऋग्वेदले उद्घोष गरेको छ- ‘एकं सद्विप्रा बहुधा वदन्त्यग्निं यमं मातरिश्वानमाहुः।’ अर्थात् सत्य भने एउटै छ, यद्यपि विद्वान्हरु यसलाई अग्नि, यम, मातरिश्वान आदि नामले पुकार्छन्। बौद्धमार्गीहरु ‘अनेकतामा एकता’-को उद्घोष गर्छन्।
सङ्ख्या–समुद्रमा असङ्ख्य नम्बर छन्। सबै नम्बर उत्तिकै महत्वपूर्ण छन्, अद्वितीय छन्। सबै नम्बरका आआफ्ना छुट्टाछुट्टै विशेषता छन्। सानोभन्दा सानोदेखि ठूलोभन्दा ठूलोसम्मका नम्बरको उत्तिकै महत्व छ।
कुनैकुनै गणितज्ञले यदाकदा नम्बरलाई चाखलाग्दो र पट्यारलाग्दो वा नीरस भनेर छुट्याउने गरेको भेटिन्छ। तर यसरी छुट्याउने वित्तिकै विरोधाभाष पैदा हुन्छ। सबैभन्दा सानो नीरस सङ्ख्या कुन हो? अहँ, यस्तो कुनै सङ्ख्या छैन। किनभने, सबैभन्दा सानो नीरस सङ्ख्या भन्ने वित्तिकै यसको खोजखबर हुने भयो। खोजखबर हुने वित्तिकै त्यो चाखलाग्दो बन्छ! अर्थात् जुनसुकै नम्बरलाई नीरस भन्नु नै त्यसलाई चाखलाग्दो बनाउनु हो, विशेष बनाउनु हो।
कुनै सङ्ख्या कसैलाई नीरस लाग्छ भने त्यही अरु कसैलाई चाखलाग्दो हुन्छ । प्रशिद्ध भारतीय गणितज्ञ रामानुजन (Srinivasa Ramanujan) र केम्ब्रिज यूनिभर्सिटीमा गणितका प्रोफेसर हार्डी (Godfrey H. Hardy) बीचको संवाद सम्बन्धी कथा भेटिन्छ। सन् १९१७मा रामानुजन सिकिस्त बिरामी भएर बेलायतको अस्पतालमा भर्ना भएका रहेछन्। रामानुजनलाई भेट्न उनका मित्र हार्डी ट्याक्सि चढेर अस्पताल पुगेछन्। कुराकानीको क्रममा हार्डीले भनेछन्- ‘आज म चढेको ट्याक्सिको नम्बर “१७२९” कस्तो बोरिङ लाग्यो। कुनै अपशकुुनको सङ्केत त होइन होला हगि?’ नम्बर सुन्ने बित्तिकै रामानुजनले बेडबाट टाउको उठाएर भनेछन्- ‘त्यसो होइन, महाशय यो त ज्यादै चाखलाग्दो नम्बर हो। दुई किसिमले दुइटा सङ्ख्याको घनमान जोडेर निस्कने यो सबैभन्दा सानो सङ्ख्या हो। ’हार्डीलाई छक्कपार्दै रामानुजनले यसका अरु दुइटा विशेषता थपेछन्- ‘यो दुई विलोमसङ्ख्याको गुणनफल हो। यो दुई त्रिकोणात्मक सङ्ख्याको वर्गअन्तर पनि हो। ’अर्थात्,
१७२९ = !# + !@# = १ + १७२८,
= (# + !)#= ७२९ +१०००।
उल्टो क्रमले बनेका सङ्ख्यालाई विलोम सङ्ख्या भनिन्छ। १९ र ९१ विलोम सङ्ख्या हुन्। यी दुईको गुणनफल १७२९ हुन्छ। क्रम नटुटाई १+२+३+ ...आदि जोड्दै जाँदा त्रिकोणात्मक सङ्ख्या बन्छ। अर्थात्,
३६ = १+२+३+४+५+६+७+८,
५५ = १+२+३+४+५+६+७+८+९+१०, अनि
५५२–३६२ = ३०२५–१२९६ = १७२९।
अर्को पक्ष पनि छ- (१+७+२+९ = १९;१७२९/१९ = ९१; १९*९१ = १७२९)।
रामानुजन र हार्डीको संवादमा आएको यो १७२९ सङख्या गणितज्ञहरुका लागि खोजको विषय बन्यो। उनीहरुले यस्तै गुण भएका अरु सङ्ख्या खोज्न थाले। तर सजिलै फेला पारेनन्। भनिन्छ, आजसम्म जम्मा छ वटा यस्ता गुण भएका सङ्ख्या पत्तालागेका छन्। कम्प्यूटरको सहायताले पत्ता लगाइएका यी सङ्ख्या एक पछि अर्को ज्यादै ठूला छन्। छैठौं सङ्ख्या २३ अङ्कले बनेको छ! यो ज्यादै ठूलो (लाख शङ्ख) सङ्ख्या हो।
गणितज्ञहरु १७२९ लाई ‘रामानुजन नम्बर’ भन्छन्। यसलाई ‘ट्याक्सिक्याब नम्बर’ पनि भनिन्छ। प्रोफेसर हार्डीले बोरिङ र अलच्छिनी भनेर मन नपराएको सङ्ख्यारामानुजनको लागि कुतूहलपूर्ण र चाखलाग्दो भयो। कथाको निस्कर्ष, रामानुजन जस्ता तीक्ष्ण सिद्धान्तीका लागि सबै सङ्ख्या उत्तिकै चित्ताकर्षक हुन्छन्।
संस्कृतमा सुभाषित अर्थात् विद्वान्को भनाइभेटिन्छ- ‘मुण्डे मुण्डे मतिर्भिन्ना कुण्डे कुण्डे नवं पयः। जातौ जातौ नवाचाराः नवा वाणी मुखे मुखे।’ अर्थात्, जति मानिस छन् त्यत्ति नै विचार हुन्छन्। एउटै गाउँमा पनि कुवा अनुसार पानीको स्वाद फरक पर्छ। एउटै संस्कारमा पनि जातिअनुसार रिवाज फरक पर्छ। एउटै घटनाको बखान पनि व्यक्तिअनुसार फरक पर्छ।
अङ्क रोजीछाडीका कुरा
‘अङ्क रोजाइ’ भनेको कुनै अङ्कले पाउने मान्यता र प्राथमिकता हो। यो कुनै अङ्क धेरै पटक भन्न रुचाउने बानी हो। कसैकसैले आफ्नै इच्छाले कुनै सङ्ख्या बताउँदा त्यसमा आफूलाई मन परेको अङ्क मिसाउँछन्। यस्तो रोजाइको असर अक्सर उनीहरुले बताउने सङ्ख्याको अन्तिम अङ्कमा पर्छ। आफूले थाहै नपाएर पनि कसैले अङ्क रोज्ने गरेको भेटिन्छ।
व्यक्तिअनुसार अङ्क रोजाइ फरक पर्छ। कसैलाई आफ्नो जन्म मितिको सङ्ख्यामा भएका अङ्कहरु मन पर्न सक्छ। कसैलाई ७ मनपर्ला,अरु कसैलाई ४ मनपर्ला। ० देखि ९ सम्मका अङ्क मध्ये धेरैजनाले ० वा ५ को अङ्क पछाडि आउने सङख्या अधिक मनपराएर रोज्ने गरेको भेटिएको छ। अक्सर ५, १०, १५, २० आदि नम्बर रोजाइमा पर्ने गरेका छन्।सामान्यतः बिजोरभन्दा जोर नम्बर बढी रोजाइमा पर्ने गर्छ। यदाकदा २ वा ६ जस्ता जोर अङ्क पनि अपेक्षागरे भन्दा बढी मात्रामा आउँछन्। कसैकसैले ८ र १२ लाई अशुभ मान्छन् र सकभर रोज्दैनन्। कसैले १३ लाई अपशकुन ठान्छन् र मन पराउँदैनन्।
अङ्क रोजाइको प्रवृत्तिले धेरै कुरामा नकारात्मक असर पार्छ। चिकित्सा विज्ञान जस्ता संवेदनीय विषयमा हुने अङ्क रोजाइको गम्भीर असर पर्छ। उदाहरणार्थ, रक्तचाप नापेर रेकर्ड गर्दा भएको अङ्क रोजाइले बिरामीको उपचारमा गम्भीर असर पार्छ। स्तन क्यान्सर जाँचमा पनि अङ्क रोजाइको विपरीत असर परेको थाहा भएको छ। स्तन क्यान्सर पत्ता लगाउन गरिएको म्यामोग्राफी अर्थात् म्यामग्राफी नाप सम्बन्धी अध्ययनमा ३८.७ प्रतिशत नतीजा शून्य वा पाँचको अङ्कमा रेकर्ड गरेको भेटिएको थियो।
पोषण सम्बन्धी सर्वेक्षणमा बालबालिकाको आन्थ्रोपोमेट्रिक अर्थात् यान्थ्रपमेट्रिक (Anthropometric) नापजोख गरिन्छ। नापजोख गर्दा अक्सर दशमलव पछाडि आएको अङ्कलाई हटाउन राउण्डिङ् गर्नुपर्ने हुन्छ। राउण्डिङ् गर्दा नजिकको आधा वा पूरा सङ्ख्यामा बढाएर वा घटाएर लेखिन्छ। यसरी राउण्डिङ् गर्दा मानव स्वभावले थाहै नपाई अङ्क रोजिने गर्छ। जस्तै- १३७ मिलिमीटरलाई कसैले बढाएर १४० बनाएर लेख्छन् भने कसैले यसलाई घटाएर १३५ मात्र लेखिदिन्छन् । यस किसिमको राउण्डिङ थोरै भएमा त्यसले मूल अनुमानमा खासै असर पार्दैन। तर बारम्बार एकतर्फी राउण्डिङ् भएमा यसबाट निकालिएको नतीजा पक्षपाती हुन्छ।
जनगणना वा पारिवारिक सर्वेक्षणमा उत्तरदाताले आफ्नो वा परिवारका सदस्यको उमेर बताउँदा अक्सर पछाडि ० वा ५ को अङ्क आउने सङ्ख्या रोज्ने गरेको भेटिएको छ। ३९ वर्ष र ४१ वर्षदुवै उमेरलाई ४० वर्ष बताउने वा लेखाउने प्रवृत्ति हुन्छ। त्यस्तै, २२-२३ वर्षका र २६-२७ वर्ष उमेरका व्यक्तिले अक्सर २५ वर्ष बताउने गर्दछन्। यस्तो प्रवृत्तिले गर्दा अन्त्यमा ५ वा ० आउने उमेर अर्थात् ५, १०, १५, ..., ३०,४५, ५० आदि वर्षमा जनसङ्ख्या झुत्ता परेर आउँछ। यस सम्बन्धी थप चर्चा परिच्छेद ६ मा गर्नेगरी यहाँ यत्तिकैमा रोकियो।
प्रत्येक नम्बर अद्वितीय व्यष्टि अर्थात् समष्टिको अंश हो। गणितमा सबै सङ्ख्या उत्तिकै महत्वपूर्ण छन् भनिन्छ तापनि केहीलाई अरु भन्दा विशेष मानिन्छ। इङ्गलिस लेखक अर्वेल (George Orwell) ले प्रसिद्ध परीकथामा सामाजिक असमानता माथि व्यङ्ग गरेका छन्- ‘सबै जनावर बराबर छन्, तर केही जनावर अरुभन्दा बढी बराबर छन्।’ यो कथनसँग मिल्दोजुल्दो देखिने गणितीय कथन भने कुनै व्यङ्ग नभएर वास्तविकतामा आधारित छ-‘सबै सङ्ख्या महत्वपूर्ण छन्, तर केही सङ्ख्या अरुभन्दा बढी महत्वका छन्।’
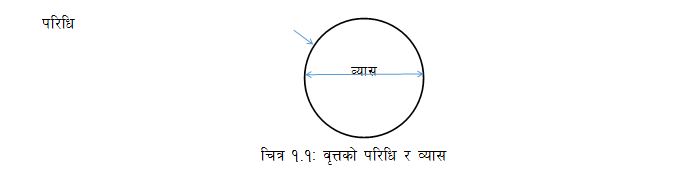
गणित विधामा महत्वपूर्ण मानिएका सङ्ख्याहरु मध्ये ‘पाइ’ (Pi) को नाम अगाडि आउँछ। पाइ भनेको कुनै वृत्तको परिधिसँग व्यासको अनुपात बताउने स्थिरअङ्क हो। वृत्त, व्यास र परिधि गणितका पारिभाषिक शब्द हुन्। ‘सिक्का’ जस्तो बाटुलो आकारलाई वृत्त भनिन्छ। परिधि भनेको वृत्तको सबैभन्दा बाहिरपट्टिको नाप हो। व्यास भनेको वृत्तको एक छेउबाट अर्को छेउसम्म जाने सबैभन्दा लामो सीधारेखा हो (चित्र १.१) ।
सूत्रमा व्यक्त गर्दा, π= परिधि/व्यास। परिधिसँग व्यासको अनुपात जनाउन गणितमा ग्रीक वर्णमालाको १६रौं अक्षर ‘π’ प्रयोग भएकोछ। पाइको अवधारणा धेरै पुरानो भए तापनि यसको प्रतीक चिह्न π अठारौं शताब्दिको शुरुदेखि प्रयोगमा आएको हो।
पाइ–लाई गणितमा असामान्य नम्बर मानिएको छ। पाइ–को अद्भुत विशेषता छ। यसको मान दशमलव पछि कुनै अङ्कमा पुगेर टुङ्गिदैन। अनन्त सम्म गैरहन्छ (π = ३.१४१५९२६५३५८९७९३...)। व्यवहारमा भने यसको मान अनन्त अङ्कमा आवश्यक छैन।
पाइ–को मान ४० अङ्कसम्म लिएमा सम्पूर्ण दृश्यमान ब्रह्माण्ड (Entire Visible Universe)को परिधि नाप्न सकिने नासाका वैज्ञानिकको दाबी छ। ब्रह्माण्डको व्याप्ति सानोतिनो छैन। यसको व्यास ७२ अर्ब प्रकाश–वर्ष भएको अनुमान छ। प्रकाशलाई वारपार गर्न यतिका वर्षलाग्ने ब्रह्माण्ड कति ठूलो होला? अनुमान गर्न पनि गाह्रो छ।
सामान्य हिसाबमा पाइ–को मोटामोटी मान ३.१४ लिएर काम चलाइन्छ। यसलाई पाइ बराबर २२/७ हुन्छ भनेर सम्झिन अझ सजिलो छ। बढी संवेदनशील हिसाबमा आवश्यकता अनुसार अङ्क सङ्ख्या बढाएर पनि लिन सकिन्छ, जस्तै π = ३.१४१६।
गणित र अरु विज्ञानका विविध सूत्रहरुमा हुने प्रयोग पाइको अर्को अद्वितीय विशेषता हो। यसको मान सधैं स्थिर वा अटल रहन्छ। अर्थात्, वृत्तको आकार ठुलो वा सानो जस्तो भएतापनि यसको मान एउटै हुन्छ। एक रुपैयाँको सिक्का होस्, नाङलो जत्रो आकृति होस्, वा ग्रह, नक्षत्रको गोलाकार आकृति होस् सबैका लागि पाइको मान उही रहन्छ।
पाइ–लाई व्यासले गुणन गर्दा वृत्तको परिधि आउँछ (वृत्तको परिधि = π*व्यास)। त्यसै गरेर, पाइ–लाई आर्धव्यासको वर्गले गुणन गर्दा वृत्तको क्षेत्रफल आउँछ (वृत्तको क्षेत्रफल =π*(व्यास÷२)२)। एक सेन्टिमीटर व्यास भएको वृत्तको परिधि करीब ३.१४ सेन्टिमीटर र क्षेत्रफल करीब ०.७८५वर्ग सेन्टिमीटर हुन्छ। त्यस्तै, एक किलोमीटर व्यास भएको वृत्तको परिधि करीब३.१४ किलोमीटर र क्षेत्रफल करीब०.७८५वर्ग किलोमीटर हुन्छ।
कसैकसैको विचारमा पाइ–को उत्पत्ति ब्रह्माण्डसँगै भएको हो। यसको लेख्य इतिहास भने चार हजार वर्ष पुरानो छ। ग्रीक दार्शनिक आर्कमिडिजले (ईशापूर्व २८७–२१२) सबैभन्दा पहिले पाइ–को मान निकालेका रहेछन्। उनले हिसाब गरेको मान चाहिँ अहिलेको जत्ति परिमार्जित थिएन। त्यसपछि चाइनिज गणितज्ञ एवं खगोलविद् चोङ्झीले (सन् ४२९–५०१) पाइको मानमा सुधार गरे। आर्कमिडिजको पालादेखि हालसम्म यसबारे अनुसन्धान जारी छ। गणितज्ञका साथै अरु वैज्ञानिकहरु यसको शुद्धता बढाउने तर्फ निरन्तर लागिपरेका छन्।
पाइ–को खोजखवरर अनुसन्धानमा पश्चिमी जगत्मात्र होइन भारतवर्षका गणितज्ञहरुको पनि उत्तिकै योगदान छ। आर्य भट्ट भन्दा पहिलेका गणितज्ञहरुमा पाइ–को स्पष्ट ज्ञान थिएन। ‘आर्यभटीय’ को ‘गणितपाद’ खण्डमा आर्यभट्टले पाइको मानबारे सिद्धान्त प्रस्तुत गरेका छन्-
चतुराधिकं शतमष्टगुणं द्वाषष्टिस्तथा सहस्राणाम् ।
अयुतद्वय विष्कम्भस्यासन्नो वृत्तपरिणाहः ।।
भावार्थ —१०० मा चार जोडेर आएको सङ्ख्या १०४ लाई आठले गुणागर्ने, र त्यसमा ६२,००० जोडे पछि २०,००० व्यास भएको वृत्तको आसन्न मान थाहा पाइन्छ। अर्थात् कुनै वृत्तको व्यास २०,००० एकाइ लामो छ भने त्यो वृत्तको परिधि लगभग ६२,८३२ एकाइ लामो हुन्छ। यो हिसाबमा, परिधि =π*व्यास, अर्थात् परिधि =३.१४१६२०,००० ≈६२,८३२ भएको हो । आर्य भट्टले वृत्तको मान ठ्याक्कै आउँदैन भन्ने जनाउन आसन्न (लगभग) शब्द प्रयोग गरेका छन्।
टेक्सस यूनिभर्सिटी (यूनिभर्सटी) का प्रोफेसर अगरवाल (R. P. Agarwal) आदिले भाष्कराचार्यले पाइ-को विभिन्न किसिमले अनुमान गरेको कुरा उल्लेख गरेकाछन् । भाष्कराचार्य १२–रौं शताब्दिका भारतीय गणितज्ञ एवं खगोलशास्त्री हुन्। उनले ‘सिद्धान्त शिरोमणि’ नामक ग्रन्थमा यसो भनेका रहेछन्-‘(३,९२७/१२५०) पाइ–को सही वा शुद्ध मान हो, (२२/७) अशुद्ध मान हो र सामान्य प्रयोगका लागि Ö१० लिँदा काम चल्छ।’ भनिन्छ, आर्यभट्ट, लिउ हुइ (Liu Hui) र चोङझीले पहिल्यै निकालेका नतीजाबाट भाष्कराचार्यका अनुमानहरु प्रभावित छन्। उनले अर्को अनुमानको पनि उल्लेख गरेका छन्- ७५४/२४०=३.१४१७।यसको स्रोत भने थाहा भएन ।
व्यासे भनन्दाग्नि हते विभक्ते खवाणासूर्यैः परिधिः स सूक्ष्मः ।
द्वाविंशतिघ्ने विहृतेऽथ शैलैः स्थूलोऽथवा स्याद्व्यवहारयोग्यः ।।
अर्थात् व्यासलाई ३९२७ ले गुणन गरेर १२५० ले भाग गर्दा आएको सङ्ख्या सूक्ष्म-परिधि हुन्छ। व्यासलाई २२ ले गुणन गरेर ७ ले भाग गर्दा आएको सङ्ख्या परिधिको व्यवहार योग्य स्थूल–मान हुन्छ।
भाष्कराचार्यले पृथ्वीको परिधि नाप्ने सरल विधि पनि उल्लेख गरेका छन्। उनको यो विधि पृथ्वीको अक्षांश र देशान्तरमा आधारित छ। उनले पृथ्वीको परिधि ४,९६७ योजन अर्थात् ३९,७३६ किलोमीटर र व्यास १,५८१ योजन अर्थात् १२,६४८ किलोमीटर निकालेका थिए। आधुनिक विधिले पृथ्वीको परिधि र व्यास क्रमशः ४०,२१२ र १२,८०० किलोमीटर निकालेको छ। भाष्कराचार्यले निकालेको र आधुनिक मानमा करीब एक प्रतिशत मात्र फरक परेको छ। भाष्कराचार्यले गरेको अनुमानमा पाइको मान ३.१४१७ आउँछ भने आधुनिक अनुमानमा ३.१४१६ आउँछ।
सर्वसाधारणको दैनिक कार्यमा पाइ उपयोगी नहुन सक्छ। तर वैज्ञानिक एवं अन्य क्षेत्रमा यसको व्यापक प्रयोग भै'आएको छ। शुरुमा वृत्तसँग एक्कासी जोडिएर आएको पाइ पछि अन्य क्षेत्रमा पनि उत्तिकै ‘विलक्षणका साथ’ देखापर्छ। वृत्तसँग स्पष्ट सम्बन्ध नदेखिएका क्षेत्रमा पनि यसको उपयोग उत्तिकै महत्वपूर्ण छ।
मूल गणितमा, वृत्तको क्षेत्रफल तथा परिधि पत्ता लगाउन पाइको उपयोग गरिन्छ। क्वान्टम फिजिक्सदेखि स्ट्याटिस्टिक्ससम्म, जिअमेट्रीदेखि कज्मलजीसम्म, जेनेटिक इन्जिनियरिङदेखि थर्मोडाइन्यामिक्ससम्म सबै विषयका अधिकांश सूत्रहरुमा पाइ देखापर्छ। आँखाको नानीदेखि इन्द्रधनुषसम्म, भवन निर्माणदेखि हवाई उडानसम्म, अनि चिकित्सा विज्ञानदेखि सङ्गीतका सिद्धान्तसम्मका क्षेत्रमा पाइ–को सहायता आवश्यक हुन्छ। अमेरिकाको अन्तरिक्ष कार्यालय नासाले अन्तरिक्षयानको प्रक्षेपण–मार्ग हिसाब गर्दा पटकपटक पाइ–को प्रयोग गर्छ।
साङ्ख्यिकीको महत्वपूर्ण सूत्रमा पाइ एक्कासि देखापर्छ। साङ्ख्यिकीमा ‘बेलकर्भ’ (Bell Curve) वा ‘नर्मलकर्भ’ (Normal Curve) नामको प्रख्यात र महत्वपूर्ण ग्राफको प्रयोग हुन्छ। वास्तविक दुनिया सम्बन्धी आँकडालाई यसले मोडेल बनाएर अध्ययन गर्छ। विशेष अवस्थामा बेलकर्भ भित्रको क्षेत्रफल ठ्याक्कै (π1/2) बराबर हुन्छ। बेलकर्भको योगुण साङ्ख्यिकीको अनुमान विधिदेखि पूर्वानुमान एवं प्रक्षेपणसम्म उपयोग गरिन्छ।
वैज्ञानिकहरु पाइ–को मानमा दशमलव पछाडिको अङ्क–सङ्ख्या सकेसम्म बढाउँदै लैजाने धुनमा खुरन्धार लागिपरेका छन्। उनीहरु थाकेका छैनन्। यो क्रम पछिसम्म जारी रहने छाँट छ। सन् २०२१ मा स्वीजरल्याण्डका वैज्ञानिकहरुले सुपरकम्प्यूटरको सहायताले एकसय आठ दिन नौ घण्टा लगाएर ६२ खरब (Trillion) भन्दा बढी अङ्कमा पाइको मान निकालेर नयाँ विश्व रेकर्ड कायम गरेको दाबी गरेका छन्।
के साँच्चै. यति धेरैै अङ्कमा पाइको मान आवश्यक छ? अहँ, व्यवहारमा पाइका यति धेरै अङ्क प्रयोगमा आउँदैनन्। ४० अङ्कले नै ब्रह्माण्डको परिधि नाप्न पुग्छ भने ६२ खरब भन्दा बढी अङ्कको के काम? भनिन्छ, दशमलव पछाडि यति धेरै अङ्क निकाल्नुको मुख्य उद्देश्य नयाँ कम्प्यूटरको क्षमता जाँच्ने हो। तर खसोखासमा, नयाँ रेकर्ड कायम गर्ने लोभ वा लालसा नै यसको कारण हो। जसरी पर्वतारोहीले सगरमाथा आरोहणको रेकर्ड तोड्न नाना चेष्टा र तमासा देखाएका छन्।
पाइ अति विस्मयकर छ। यसबारे तरह तरहका अनौठा काम भएका छन्। जस्तै- सन् २०१५ मा भारतको राजवीर मीना भन्ने व्यक्तिले ७० हजार अङ्कसम्म पाइ–को मान कण्ठस्थ सुनाएर गिनिजबुकमा नाम लेखाए। फ्रान्स र इटलीमा पाइ–का अङ्क देखाउन मानव सञ्जाल बनेका छन्। कसैले पाइ–को गीत गाएका छन्। कसैले पाइ नामको सिनेमा बनाएका छन्।
अमेरिकी भौतिकशास्त्री ‘श’ (Larry Shaw) ले पहिलो पटक सन् १९८८ मा ‘पाइदिवस’ आयोजना गरे। पाइ–को छोटकरी मान ‘३.१४’ लाई सन्दर्भमा राखेर ईसवी सन्को तेस्रो महिनाको १४ तारिख (मार्च १४) का दिन यो दिवस मनाइन्छ। सन् २००९ मा अमेरिकी प्रतिनिधि सभाले यो दिवसलाई सरकारी मान्यता पनि दियो। पाइ दिवस मनाउने प्रचलन आजसम्म कायमै छ। पाइ परिकार खाएर यो दिवस मनाइन्छ । मुछेको पीठोको भित्रपट्टि गुभोमा फलपूmल, मिठाई, किसमिस बदाम हालेर पकाएको कचौडी वा ढोसेरोटो जस्तो परिकारलाई पाइ भनिन्छ। चाखलाग्दो कुरा के छ भने आइन्स्टाइनको जन्म दिन (१४ मार्च, १८७९) पनि ‘पाइ डे’–मा पर्छ।
गणितका प्रोफेसर स्टेवार्ट (Ian Stewart) ले आफ्नो पुस्तक ‘Incredible Numbers’–मा भनेका छन् —‘पाइ–का सम्बन्धमा ब्रह्माण्डले हामीसँग वास्तवमा क्रूरचाल चालेकैहोः यति महत्वपूर्ण नम्बरलाई हामी दशमलवमा पूरापूर लेख्न सक्तैनौं ।जटिल सूत्रको मद्दतविना यसको हिसाब निकाल्न सकिन्न। जतिसुकै वाधा अड्चन भए तापनिवैज्ञानिकका लागि यो नम्बर चित्ताकर्षक र रहस्यपूर्ण नै छ ।’
‘आजसम्म कुनैपनि नम्बर प्रणालीले पाइ–लाई कब्जामा लिन सकेको छैन।’
अमेरिकन गणितज्ञ प्रोफेसर क्यास्नर (Edward Kasner)को नौवर्षे भतिजो (भानिज?) मिल्टन (Milton Sirotta) सम्बन्धी रोचक कथा भेटिन्छ। मिल्टनलाई ‘गूगोल’ (Googol) को आविष्कारक मानिन्छ। मिल्टनसँग टहलिँदै गर्दा क्यास्नरले उनलाई सोधेछन्-‘एक अङ्कको पछाडि सय ओटा सुन्ना भएको असाध्यै ठूलो सङ्ख्याको नाम के होला?’ जवाफमा मिल्टनले भनेछन्- ‘यतिठूलो सङ्ख्या त गूगोल (Googol) हो’। मिल्टनको सुझाव क्यास्नरलाई मन परेछ। यस बाहेक,मिल्टनले गूगोल भन्दा ठूलो सङ्ख्याको नाम‘गूगोलप्लेक्स’ (Googolplex) राख्ने पनि सुझाव दिएका रहेछन्।
मिल्टनको सुझावअनुसार सन् १९२० मा आफूले गूगोल र गूगोलप्लेक्स दुई शब्दको नामकरण गरेको कुरा सन् १९४० ताका प्रकाशित पुस्तकमा क्यास्नरले उल्लेख गरेका छन्। गूगोललाई अङ्कमा लेख्दा ‘१ अङ्कको पछाडि सय ओटा सुन्ना’ लेखिन्छ (‘१०१००’)। अनि गूगोलप्लेक्सलाई यसरी जनाउनु पर्छऔ ‘१०गुगोल’ । शुरुमा गूगोलप्लेक्सलाई १ अङ्कको पछाडि नथाकेसम्म ० लेख्दा हुन आउने अति ठूलो सङ्ख्या मानिएको थियो।
गूगोलसँग जोडिएको अर्को कथा छ। भनिन्छ, स्ट्यानफोर्ड यूनिभर्सिटीमा पीएचडीको तयारी गरिरहेका दुई विद्यार्थी ब्रिन Sergey Brin)र पेज(Larry Page) ले सन् १९९५ ताका वेब पेज (World Wide Web or www)मा भएका सामग्री खोज्न सजिलो हुने ‘सर्च इन्जिन’ बनाए। उनीहरुले त्यसको नाम ‘ब्याकरब (BackRub) राखेछन्। त्यसपछि सन् १९९८ को मध्यतिर उनीहरुले क्यालफोर्नियाको मेल्नोपार्कमा ‘गूगल’नाम राखेर पसल खोलेछन्।
शुरुमा उनीहरुले पसलको नाम गूगोल (अर्थात् ज्यादै ठूलो सर्च इन्जिन) राख्ने योजना बनाएका रहेछन् तर वर्णविन्यासमा गल्ती भएर ‘गूगल’ (Google) पो लेखिन पुगेछ। सन् २००४ मा सर्वसाधारण समेत सहभागी भएको गूगल नामको कम्पनी स्थापना भयो। अहिले यो सर्च इन्जिन सबैभन्दा बढी चल्तीमा छ। यसलाई सबैभन्दा राम्रो सर्च इन्जिन मानिन्छ। यसले ९० प्रतिशत भन्दा बढी बजार लिएको दाबी गरिएको छ। गूगोल र गूगल सम्बन्धी छोटकरी कथा यत्ति नै ।
नम्बर र साङ्ख्यिकी एकआपसमा सम्बन्धित छन्। एउटा कक्षाका प्रत्येक विद्यार्थीको उचाइ नापेर आएको लगतबाट हिसाब गरेर कक्षाका विद्यार्थीको औसत उचाइ निकालिन्छ। यो उदाहरणमा प्रत्येक विद्यार्थीको उचाइ छुट्टै आँकडा हो। उचाइको लगत (जम्माजम्मी विवरण) आँकडा समूह (Data Set) हो। लगत प्रशोधन गरेर निकालिएको विद्यार्थीको औसत उचाइ चाहिँ साङ्ख्यिकी (Statistics) हो। त्यस्तै, रुखको फेदको गोलाइ नापबाट आँकडा बन्छ। गोलाइको लगतबाट हिसाबगरेर वनक्षेत्रमा भएका रुखको औसत गोलाइ निकाले पछि साङ्ख्यिकी बन्छ। यसरी उत्पादित साङ्ख्यिकीलाई टेबल, चार्ट वा ग्राफको माध्यमबाट प्रस्तुत गर्न सकिन्छ।
साङ्ख्यिकीलाई फगत नम्बर हो भनेर होच्याइएको प्रसङ्ग साहित्यमा भेटिन्छ। यो कथाको आधिकारिकता भने पुष्टि भएको छैन। दोस्रो विश्वयुद्ध सकिएको एक वर्ष पछि तत्कालीन सोभियत रुसको युक्रेनमा ठूलो अनिकाल परेको रहेछ। भोकमरीले धेरैको ज्यान लिएछ। त्यस बखत सोभियत रुसमा कुख्यात तानाशाह स्टालिन प्रधानमन्त्री थिए। युक्रेनको भोकमरीबारे मीटिङमा एकजना अफिसरले खान नपाएर लाखौं मानिसहरु मरेको दुःखद घटनाको विवरण प्रस्तुत गर्दै रहेछन्। विवरण प्रस्तुत गरिरहेकै बेला स्टालिनले उनलाई बीचमै रोकेर भनेछन् ‘भोकले एकजना मात्र मर्यो भने त्यो दुःखद घटना हुन्छ; यदि लाखौं मरेभने त्यो साङ्ख्यिकी मात्र हो’। यस्ता संवेदनाविहीन अभिव्यक्तिले साङ्ख्यिकीको उपादेयतामा नकारात्मक असर पार्छ।
चार्ली च्याप्लिनले …Monsieur VerdousÚ नामको सिने–संबादमा यस्तो व्यङ्ग्य गरेका थिए- ‘एकजनालाई मार्ने खलनायक (भिलियन) हुन्छ, लाखौंलाई मार्ने नायक हुन्छ। मेरा असल मित्रहरु, नम्बरले पाप पखाल्छ।’
तर त्यसो होइन। नम्बरहरु अद्भुत छन्, यत्र–तत्र–सर्वत्र व्याप्त छन्, विश्वव्यापी छन्, चमत्कारी छन्। नम्बर विनाको संसार कल्पना बाहिर छ। हेर्न जान्नुपर्छ, नम्बर जताततै देखिने छन्। कोभिडको सङ्क्रमण दरदेखि महँगीदरसम्म, न्याय प्रणालीदेखि इन्टरनेट प्रणालीसम्म नम्बर जताततै व्याप्त छ। प्रयोग गर्न जान्नुपर्छ, नम्बरले हाम्रो जीवनमा सुधार ल्याउन मद्दत गर्छ।
नम्बर सञ्चार जगत्को शक्तिशाली तथा प्रेरक औजार हो। वाणिज्य, व्यवसायको फाँटमा पनि नम्बर अमूल्य औजार साबित भएको छ। नम्बरले जस्तो मीठो ढङ्गले अरु केही कुराले काम गर्दैन। यसका दोष वा सीमा पनि छन्। नम्बरसँगै हिड्दा धेरै खाल्डाखुल्डी पनि भेटिन्छन्। नम्बरलाई विनाविवेक प्रयोग गर्दा यसबाट हानि हुनसक्छ। छापामा आएका नम्बरलाई मानिसले विश्वास गर्छन्। स्वार्थका लागि अजेण्डा अघिसार्नेहरुले ‘डेटाह्याक’ (DataHack), सूचनाको ‘सुरक्षा विखण्डन’, नम्बरलाई तलमाथी पार्ने जस्ता बिजाइँ गर्ने गरेको भेटिएको छ। यस्ताले सत्यलाई तोडमरोड गरेर स्वार्थ सिद्धिका लागि गलत व्याख्या गरेका हुन्छन्।
यस सन्दर्भमा मार्क ट्वीनको भनाइलाई केही बदलेर यसो भन्न सकिन्छ — साङ्ख्यिकीले ढाँट्दैन, ढँटुवाले यसलाई तोडमरोड गर्छ ।साङ्ख्यिकीको विशाल फाँटमा नम्बर प्रवेशद्वार हो । साङ्ख्यिकीका विविध पक्षमा नम्बर जोडिएर आउँछ र यसको केन्द्रसम्म पुग्छ ।
नेपाली साहित्यमा अति रुचाएर पढिएको निबन्ध ‘के नेपाल सानो छ ?’–मा महाकवि देवकोटाले भनेका छन्- ‘नेपाल। सुन्दर शान्त विशाल।’ ’नेपाल कति विशाल छ त? यो प्रश्नको उत्तर नम्बरका माध्यमले खोजौं। संयुक्त राष्ट्र सङ्घमा हाल १९३ देश सदस्य छन्। क्षेत्रफलको दृष्टिले नेपाल ९३औं स्थानमा छ, अर्थात् १०० देशहरु नेपालभन्दा साना छन्। हाल अनुमानित जनसङ्ख्याको हिसाबले नेपाल १४४ देशभन्दा ठ्रलो छ। जनघनत्वका दृष्टिले नेपाल १४५ देशभन्दा ठूलो छ।
देश सानो छ वा ठूलो छ भन्ने कुरा प्रस्तुत विषयको सापेक्षतामा भरपर्छ। कुनै विषयमा तुलना गर्दा नेपाल ठूलो हुन्छ भने कुनै अर्को विषयमा तुलना गर्दा सानो हुन्छ। क्षेत्रफल वा हालको अनुमानित जनसङ्ख्याका दृष्टिले चीन वा भारतको तुलनामा नेपाल ज्यादै सानो हो। अर्कोतर्फ, भुटान वा माल्दिभ्ससँग तुलना गर्दा नेपाल धेरै ठूलो हो। जनघनत्वका हिसाबमा चीन नेपालभन्दा पछाडि (सानो) छ तर माल्दिभ्स नेपालभन्दा अगाडि (ठूलो) छ। क्षेत्रफलका दृष्टिले नेपाल र बाङ्गलादेश लगभग बराबर छन् तर बाङ्गलादेशको जनसङ्ख्या नेपालकोभन्दा करीब ५.६ गुणा बढी छ। अर्थात् क्षेत्रमा दुवै तुल्य भए तापनि जनसङ्ख्याका दृष्टिले बाङ्गलादेश नेपालभन्दा ठूलो छ। नम्बरविना यसरी सजिलोसँग तुलना गर्न सकिने थिएन।

(यो लेख ‘तथ्याङ्क कि साङ्ख्यिकी?’ पुस्तकका लेखक बास्तोलाको अनुमतिमा प्रकाशित गरेका हौं। पुस्तकमा यसको शीर्षक ‘नम्बरहरु अद्भुत र व्यापक छन्!’ छ। -सम्पादक)
 सर्च गर्नुहोस्
सर्च गर्नुहोस्

